Conjugated Organic Molecules
Chemistry Overview
Atomic Orbitals
It is necessary to first present a quick overview of standard chemistry to explain what conjugated systems are and how they occur. For starters, it is important to understand that chemistry is primarily the study of the electronic structure of atoms, not their nuclear or sub-nuclear properties, and so chemists chiefly concern themselves with how electrons behave and interact with each other and nuclei, mostly neglecting inter-nuclear forces. As such, an important part of determining the shape of atoms and molecules is knowing the electronic configuration; that is, where the electrons are localized in space around the nuclei. From quantum theory, however, a small particle like an electron cannot have a definite position, and instead is smeared out around the atom (molecule) as a wave-like entity in a probability distribution ("electron cloud") that determines the probability density that an electron will be found in a particular region of space. For example, the Schrödinger equation for the hydrogen atom gives the ground state wavefunction (wave-like state of the electron in space) as \[\psi(r)=\frac{1}{\sqrt{\pi}a_0^{3/2}}e^{-r/a_0}\] The probability of finding the electron at position \(r\) is just the square of the wavefunction.
The spherical nature of this ground (lowest energy)
state constitutes what is called an "s - orbital"; in
particular, the lowest spherical orbital (electronic wavefunction
about an atom) is called the 1s orbital. The next highest
energy spherical orbital is the 2s orbital, and so on. The
integer preceding the orbital type is usually denoted n and
is referred to as the principal quantum number. As
this number increases, though, there can be other shapes of allowed
solutions to the Schrödinger equation. The s - orbitals
correspond to the electron having no total angular momentum; as n
increases, the orbital quantum number
\(\ell\) is allowed to take on other values. For \(\ell=0\), we have
s - orbitals; for 
we have p - orbitals
(dumbbell shaped); for 
we have d - orbitals, with
larger and larger values being more complicated in shape. For each
value of n, any integer less than n (but greater
than or equal to zero) is valid for 
. In addition, each
value lends itself to multiple subshells: for s - orbitals,
there is only one orientation for a sphere, so that the
magnetic quantum number m is zero. For
higher , m
can take on values 
in integer steps.
Hence for p - orbitals,
m can be 1, 0, or -1, corresponding to the three
orientations of the dumbbell-shaped orbitals shown below.
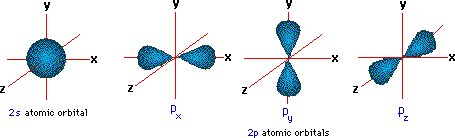
The energies of these shells (orbitals) are represented diagrammatically to the right. According to the Pauli Exclusion Principle, Hund's Rules, and the Aufbau Principle, as we add electrons to an atom we fill the lowest energy first, and place only two electrons in each subshell (one with its spin up, one down). As we reach degenerate subshells (like the 2p shells), we first place an unpaired electron in each configuration, then begin to pair the remaining ones.
Now we ask how molecules can form that have orbital
geometries that do not match those required to form a 
or 
bond, such as trigonal or tetrahedral configurations. The answers is that the orbitals can hybridize, forming
mixtures of s and p orbital characteristics to
properly bond. Below is shown a hybrid orbital that results when an
s orbital and all three of the p orbitals interact on
the same atom to form an sp3 hybrid orbital. The positive
and negative phases of the orbitals is important to explain
the constructive and destructive nature of interacting
wavefunctions.
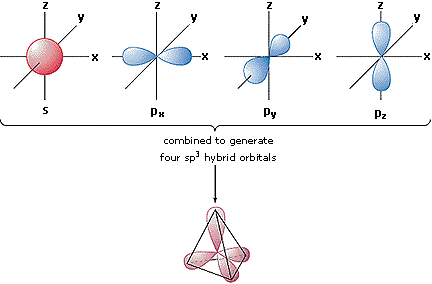
An s orbital can also interact with one or two p orbitals to obtain other hybridizations (sp, sp2). These hybrid orbitals allow atoms to adopt geometric bonding configurations that would otherwise be unexplained by the shapes of the regular s and p orbitals. The three types of s-p hybrid orbitals are called linear, trigonal, and tetrahedral, and we must remember that the molecule formed from the bonding of these orbitals will take that shape including all electrons involved, even if they aren't involved in the bond. Hence ammonia, even though a central nitrogen is bound to three hydrogens, maintains a pyramidal shape, not a trigonal one, since the non-bonding electrons still occupy one of the sp3 orbitals.
Molecular Orbitals
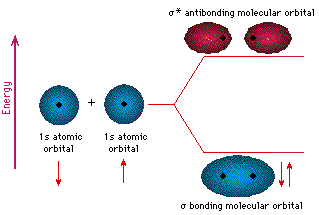
Now let's see what happens when two atoms interact
to form a molecule. One method of interacting is to create a
chemical bond: the two (wavelike) electron clouds of the reacting
atoms combine either in phase to create a bonding molecular
orbital or out of phase to create an antibonding
molecular orbital. Orbitals that lie along the bond axis
are called
bonds, while those that form off of the axis are
bonds. Below is a diagram of two interacting hydrogen atoms. When
their wavefunctions overlap, the 1s orbitals can form a
bond or a 
bond (the asterisk denotes an antibonding orbital).
Both electrons fill the lower energy orbital, so that H2 is a
stable molecule.
Not only s orbitals can form
bonds; p orbitals can as well, as shown in figure A below for F2,
as well as hybrid orbitals, as shown in part B of the figure for sp3
hybridized atoms, such as the carbons in ethane (C2H6).
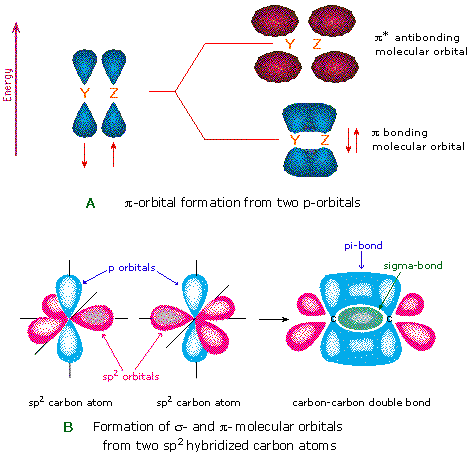
Another type of bond is the
bond, formed by laterally overlapping p orbitals. These bonds are
exclusively formed by regular p orbital overlaps off-axis,
and not by hybrids or s orbitals. An example is shown below
for the carbons of ethene.
It is these
bonds that make double or triple bonds: one from the
bond, and one from each bond
in the perpendicular directions. When these bonds are created, the
two individual atoms form a molecule, and the resulting combined
orbitals are called molecular orbitals (MO's).
Below are the MOs for difluorine, dinitrogen, and dioxygen (click on the
diagram).
Notice that for nitrogen, there is a flipping of
the relative orders of the 2p
bond and the
bonding orbitals. This relates to the fact that there is additional
s-p hybridization going on, changing the relative energies.
Also notice that oxygen has two unpaired electrons in it's highest
occupied molecular orbital (HOMO), indicating that there is a net
spin to the oxygen molecule, which gives it its paramagnetic
properties.
Conjugation
We now turn our attention to conjugated
systems, which possess a carbon backbone with alternating
single and double bonds. Whenever there are three or more parallel
p orbitals interacting in a type bond, the electrons
of the bonds are delocalized and shared among the carbon atoms, each
of which is hybridized in the sp2 configuration. When
these -bonds are combined (ignoring the
bonds), there
result three possible MO's (in order of increasing energy): is
bonding and has no nodes, 
is nonbonding and has one node, and
is antibonding with two nodes.
Diagrams of these cases are shown below.
Typically, molecular orbital transitions emit and absorb photons in the UV and visible spectrum, with longer wavelengths corresponding to vibrations, translations and rotations of the entire molecule and shorter wavelengths corresponding to ionization and destruction of the molecule. Only in the narrow bandgap of 200-800 nm do we find orbital excitations, and hence, light interactions. In the figure below, the usual transitions are shown, with only the leftmost two taking place in the visible range (400-800 nm).
As we add more conjugated double bonds to the system, there become more and more molecular orbitals, and the energy gap between the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) decreases, meaning that light with longer wavelengths are absorbed. Click on the picture below to see how this occurs.
Conjugated systems need not be linear, though, and can be extended organic structures with rings, alkyl groups and polar additions. Any molecule or part of a molecule that is responsible for the molecule's color is called a chromophore. The absorption spectra of these molecules is, in general, rather complicated, since UV/visible light gets scattered quite a bit more than higher energy photons. Hence the spectral peaks can be quite broad, as opposed to those on an NMR scan. Nevertheless, a set of empirical rules called the Woodward-Fieser rules (on next page) can let us estimate the maximal absorbed frequency for a conjugated system (if we cannot just directly measure it). Each additional moiety added to a base compound shifts the peak to a longer wavelength. As the peak absorption wavelength reaches the visible spectrum (about 400-750 nm), the molecule becomes colored. The wavelength that is absorbed is removed from the reflected/scattered light, and we see the complementary color.
For example, let us examine the β-carotene molecule, shown below.
The Woodward-Fieser rules (or just looking it up) let us determine the absorption peak to be 455 nm, a blue-cyan color. The complementary color (across the color wheel shown below) is a reddish-orange, which explains why carrots, with a natural abundance of β-carotene, are usually orange.
For more examples of colored chemicals, click here.
Thanks to The Causes of Color and The Virtual Textbook of Organic Chemistry for information and use of graphics.