Differential Equations

Nearly all problems in physics can be reduced to solving some form of differential equation, often linear. Here I shall go over some of the methods of solutions for Laplace's equation, the Helmholtz equation, various special functions, the diffusion equation, and the wave equation, in a variety of coordinate systems.

Laplace's Equation

The Laplace equation, $\nabla^2\phi(\mathbf{r})=0$ , is at the heart of many physical laws, often arising in potential theory when a source of the potential is absent. The solutions to Laplace's equation are called harmonic functions, and possess special properties, such as the fact that the average value of the functions over a spherical surface is equal to the value at the center of the sphere (Gauss's Harmonic Function Theorem). In general, at least within 13 coordinate systems, the solutions can be found by the method of separation of variables. 10 of these are special cases of the confocal ellipsoidal coordinate system, including the common Cartesian, cylindrical, and spherical systems. For example, consider the Cartesian version of the equation:

$\frac{\partial^2\phi}{\partial x^2}+\frac{\partial^2\phi}{\partial y^2}+ \frac{\partial^2\phi}{\partial z^2}=0$

We can split the partial differential equation into ordinary differential equations using the ansatz that the solution is the product of functions dependent only one one variable: $\phi(x,y,z)=X(x)Y(y)Z(z)$ , so that if we divide through by $\phi=XYZ$ , we have:

$\frac{1}{X}\frac{d^2X}{dx^2}+\frac{1}{Y}\frac{d^2Y}{dy^2}+\frac{1}{Z}\frac{d^2Z}{dz^2}=0$

Since each coordinate may be varied independently of the others, each term must in fact be equal to a constant. We choose the constants so that

$\frac{1}{X}\frac{d^2X}{dx^2}=-l^2,\; \frac{1}{Y}\frac{d^2Y}{dy^2}=-m^2,\; \frac{1}{Z}\frac{d^2Z}{dz^2}=-n^2=l^2+m^2$

These three ODEs can be solved based on the boundary conditions imposed (in general they will be sines, cosines, and exponentials for Cartesian systems). Our solutions are then labeled by these eigenvalues:

$\phi_{lm}(x,y,z)=X_l(x)Y_m(y)Z_n(z)$

such that . Because Laplace's equation is linear, the most general solution is a linear superposition of solutions, so that we may write our general solution as

$\Phi=\sum_{l,m}a_{lm}\phi_{lm}$

where the constant coefficients $a_{lm}$ are chosen to satisfy the boundary conditions, leading to a discrete set of the eigenvalues .

Another often-used system of coordinates for systems with axial symmetry is the cylindrical coordinate system. Here we again use separation of variables using the ansatz $\phi(r,\theta,z)=R(r)\Theta(\theta)Z(z)$ . The Laplacian in these coordinates is

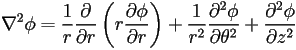
$\nabla^2\phi=\frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial\phi}{\partial r}\right)+\frac{1}{r^2}\frac{\partial^2\phi}{\partial\theta^2}+\frac{\partial^2\phi}{\partial z^2}$

which upon substitution into Laplace's equation reduces to

$\frac{1}{Rr}\frac{d}{dr}\left(r\frac{dR}{dr}\right)+\frac{1}{\Theta r^2}\frac{d^2\Theta}{d\theta^2}+\frac{1}{Z}\frac{d^2 Z}{dz^2}=0$ .

Since the dependence has been isolated, let's set it equal to a constant: $\frac{1}{Z}\frac{d^2 Z}{dz^2}=k^2$ . Then after some rearrangement,

$\frac{r}{R}\frac{d}{dr}\left(r\frac{dR}{dr}\right)+\frac{1}{\Theta}\frac{d^2\Theta}{d\theta^2}+r^2k^2=0$ ,

so we've isolated the angular dependence. Set $\frac{1}{\Theta}\frac{d^2\Theta}{d\theta^2}=-m^2$ , anticipating sines and cosines. The remaining equation for the radial dependence,

$r^2\frac{d^2 R}{dr^2}+r\frac{dR}{dr}+(k^2r^2-m^2)R=0$ ,

is called Bessel's equation, and the solutions are the Bessel functions and . So we have that $R_{km}(r)=A_{km}J_m(kr)+B_{km}N_m(kr)$ , $\Theta_m(\theta)=C_m\cos m\theta+D_m\sin m\theta$ , $Z_k(z)=E_ke^{kz}+F_ke^{-kz}$ , and again a general solution is a linear combination of these.

The third important coordinate system is the spherical system, where $\psi(r,\theta,\phi)=R(r)\Theta(\theta)\Phi(\phi)$ . The Laplacian is

$\nabla^2=\frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial}{\partial r}\right)+\frac{1}{r^2\sin^2\theta}\frac{\partial^2}{\partial\phi^2}+\frac{1}{r^2\sin^2\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial}{\partial\theta}\right)$ ,

so that using our ansatz,

$\sin^2\theta\left(\frac{r^2}{R}\frac{d^2R}{dr^2}+\frac{2r}{R}\frac{dR}{dr}\right)+\frac{1}{\Phi}\frac{d^2\Phi}{d\phi^2}+\left(\frac{\cos\theta\sin\theta}{\Theta}\frac{d\Theta}{d\theta}+\frac{\sin^2\theta}{\Theta}\frac{d^2\Theta}{d\theta^2}\right)=0$ .

The $\phi$ dependence has been isolated, so set $\frac{1}{\Phi}\frac{d^2\Phi}{d\phi^2}=-m^2$ . Hence

$\frac{r^2}{R}\frac{d^2R}{dr^2}+\frac{2r}{R}\frac{dR}{dr}+\frac{1}{\sin^2\theta}\left(\frac{\cos\theta\sin\theta}{\Theta}\frac{d\Theta}{d\theta}+\frac{\sin^2\theta}{\Theta}\frac{d^2\Theta}{d\theta^2}-m^2\right)=0$ .

The radial part must equal a constant, so we write $r^2\frac{d^2R}{dr^2}+2r\frac{dR}{dr}=l(l+1)R$ , which has the solutions $R_l(r)=A_lr^l+B_lr^{-l-1}$ . The remaining angular piece is

$\Theta''+\cot\theta\Theta'+\left[l(l+1)-\frac{m^2}{\sin^2\theta}\right]\Theta=0$ ,

known as the associated Legendre differential equation in $\cos\theta$ , and whose solutions are the polynomials $P_l^m(\cos\theta)$ . The general complex solution is then

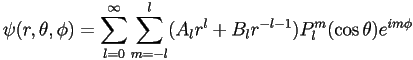$\psi(r,\theta,\phi)=\sum_{l=0}^{\infty}\sum_{m=-l}^l(A_lr^l+B_lr^{-l-1})P_l^m(\cos\theta)e^{im\phi}$ .

The angular dependence can be summarized by defining the spherical harmonics,

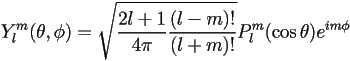$Y_l^m(\theta,\phi)=\sqrt{\frac{2l+1}{4\pi}\frac{(l-m)!}{(l+m)!}}P_l^m(\cos\theta)e^{im\phi}$ ,

where the normalization constant is chosen so that the spherical harmonics are orthogonal over all solid angle.

Under Construction

Under Construction

The Quantum Immortal

Differential Equations

Laplace's Equation