Hyperbolic Geometry
I've always been fascinated by the calculus of manifolds, particularly the rare and interesting cases. A while ago I prepared the following information about hyperbolic space as part of a presentation on the subject.
The Notion of Parallel

When Euclid formulated the postulates of geometry over 23 centuries ago, he supposed that through any point not on a line, exactly one line could be drawn that did not intersect the line. This was the famous "Fifth Postulate," which inevitably proved correct only under certain further assumptions about the space in which the "line" was drawn. In the figure to the right, line \(\ell\) is parallel to line \(m\) through point \(P\).
But what do we mean by a "line"? From the field of differential geometry, what we really mean is a geodesic, a curve in space that has zero geodesic curvature and is stationary with respect to arc length. This means that a geodesic will always have either minimum or maximum length between two given points in space (we usually are only concerned with the minimizing case). In Euclidean (flat) space, this is a straight line, and we know that the shortest distance between two points in this space (denoted \(\mathbb{R}^n\) where \(n\) is the dimension of the space) is a segment of this line.
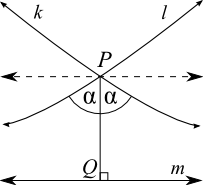
Can there be other spaces where Euclid's Fifth Postulate does not hold? Yes, there can. Ancient geometers were often troubled by the axiom, and by the 18th century several alternative geometries were established. Among these was the notion of hyperbolic geometry. Replacing the Fifth Postulate was a different axiom: through any point \(P\) not on line \(m\), there exist at least two lines that do not intersect \(m\). In the figure to the left, lines \(k\) and \(\ell\) intersect the perpendicular through \(P\) at angle \(\alpha\), but do not intersect \(m\) itself (the lines actually curve in hyperbolic space). If \(\alpha\) is the minimum such angle, then the lines \(k\) and \(\ell\) are said to be asymptotic to \(m\), meaning that they intersect at infinity. At any larger angle, the lines are called ultraparallel, and never intersect \(m\), even at infinity. Note that there are an infinite number of ultraparallel lines, but only two asymptotic lines to a given line through a point not on it.
Models of the Hyperbolic Plane
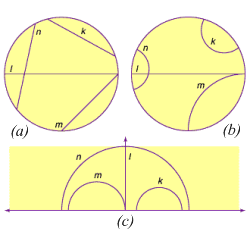
As hyperbolic space \(\mathbb{H}^n\) is not our familiar \(\mathbb{R}^n\), it can be difficult to envision it, though they are diffeomorphic. There are three standard models for visualizing hyperbolic space: the Klein-Beltrami Model, the Poincaré Disk Model, and the Half-Plane Model. These are shown as (a), (b), and (c) to the left. Notice that (b) and (c) look rather similar in that if the bounding circle of the disk model was cut and straightened into a line, it would be the \(x\)-axis of the half-plane. Even the shapes of the geodesics shown (\(k\), \(\ell\), \(m\), and \(n\) in the figure) are preserved in this transformation. This is what is known as a conformal mapping: angles are preserved, even if distances are not. It is due to a powerful theorem called the Riemann Mapping Theorem that any simply connected open subset of \(\mathbb{C}\) which is not all of \(\mathbb{C}\) is conformal to the unit disk \[D=\{z\in\mathbb{C}:|z|\leq 1\},\] including the upper half-plane \[\mathbb{H}^2=\{(x,y)\in\mathbb{R}^2:y>0\}=\{z\in\mathbb{C}:\Im[z]>0\}.\] Due to the natural isomorphism between \(\mathbb{C}\) and \(\mathbb{R}^2\), I will often refrain from making a distinction between the two planes. Generally coordinates in \(\mathbb{R}^2\) will be denoted \((x,y)\), while in \(\mathbb{C}\) I will just use the complex number \(z\).
Let's begin by looking at the hyperbolic half-plane \(\mathbb{H}^2\). In the figure, we can see what appear to be circles and rays extending from the \(x\)-axis, which I claimed were geodesics. To prove this statement, we need to examine arc lengths in the half-plane. In this model, the metric has the form \[ds^2=\frac{dx^2+dy^2}{y^2},\] which is a bit different from the Euclidean metric \(ds^2=dx^2+dy^2\). Nevertheless, our tools from calculus will still help us out, so let's say that one type of geodesic really is a circle on the \(x\)-axis. We will parameterize with the angle \(\theta\) in the setup shown below:

Geodesics
Our coordinates are chosen to be:

so that the arc length along \(PQ\) is:

Also, for a vertical line segment, we can calculate the length:
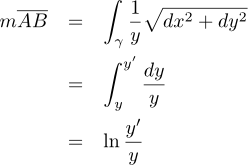
In the complex case, we note that

so that using the same method of derivation we can find the hyperbolic distance between two points:

Hence the general distance between two points in \(\mathbb{H}^2\) is \[d[(x_1,y_1),(x_2,y_2)]=\cosh^{-1}\left[1+\frac{(x_1-x_2)^2+(y_1-y_2)^2}{2y_1y_2}\right].\] Also note that we can show that these semicircles and vertical rays are geodesics by considering general path lengths in \(\mathbb{H}^2\):

Let's examine what a curve would look like in \(\mathbb{H}^2\) if it were the locus of points a constant distance (1, say) from a vertical ray.
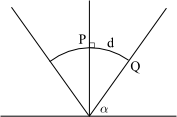
The curves would have to be separated by a geodesic (arc of semicircle) as shown in the drawing, hence we have:
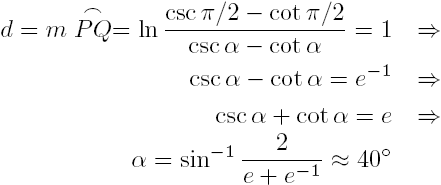
so that the curve of constant distance is actually a Euclidean ray! It can also be shown that the locus of points a given distance from a semicircular geodesic is a circular arc with the same endpoints as the semicircle (though not necessarily orthogonal to the \(x\)-axis). In fact, sets of points of constant distance to a geodesic in any model of the hyperbolic plane are called hypercycles, and in the half-plane model these are lines and arcs of circles that cut the \(x\)-axis at non-right angles.
Circles in the Half-Plane

It is an interesting fact that circles in Euclidean space are mapped to circles in hyperbolic space, though the dependence of the circumference on the diameter is highly non-linear. In mapping a Euclidean circle to a hyperbolic circle, we see that the center is shifted downward, so that \(H=h\), and from the metric,
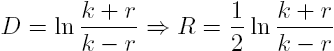
so that \(k=K\cosh R\), \(r=K\sinh R\), and \(K=\sqrt{k^2-r^2}\). If we parameterize by \(\theta\), we can write \(x=h+r\cos\theta\) and \(y=k+r\sin\theta\), so that
 ,
,
and since \(\tan^{-1}x+\tan^{-1}\tfrac{1}{x}=\tfrac{\pi}{2}\), we have that the hyperbolic circumference is \(\tfrac{2\pi r}{\sqrt{k^2-r^2}}\).
Next Page |