Hyperbolic Geometry Continued (Page 2)
Hyperbolic Area
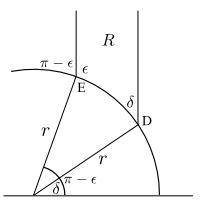
To find the area of the region \(R\) as shown to the left, we use the hyperbolic area \[A(R)=\iint_R\frac{dx\,dy}{y^2}\] so that

We can see from this that the hyperbolic area of a region bounded by two vertical geodesics and a single non-vertical geodesic (on the side extending to positive infinity) depends only on the so-called defect, the difference in interior angles from \(\pi\). This region can be thought of as a triangle with one vertex at infinity. This is what is known as an ideal vertex. We can see that if vertical geodesics were drawn from the points of intersection of a semicircular geodesic with the \(x\)-axis, the area of this ideal triangle (having three ideal vertices) would be exactly \(\pi\), though each of its interior angles would be zero.

In the figure to the right, we have drawn a triangle bounded by three geodesics (as any triangle must be). To find the area of this triangle, we just subtract the area of \(S\) from the area of \(R\) (the whole region above the lower semicircle), which we can do by using the method and formula derived above to give us again that the area is exactly the defect in interior angular measure (we leave it as an exercise to show that this is true for any triangle, even if not bounded by a vertical geodesic).

Hyperbolic Trigonometry
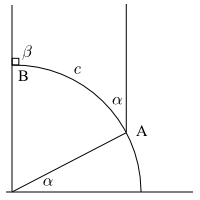
Trigonometry in \(\mathbb{H}^2\) is really not too different from trigonometry in Euclidean space, at least on small scales. The term still refers to the study of triangles, their angles and side lengths. In the figure on the left, we can use the properties of geodesic arc length to find the relationship between arc length and angle measure:

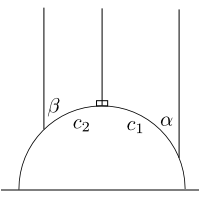
When we have non-right angles, we can break the bounding arc into segments and apply the sum identity for the hyperbolic sine function:

Right Triangles
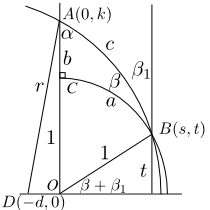
We now turn our attention to one of the most important geometric objects from Euclidean geometry: the right triangle. A triangle on any Riemannian manifold can be thought of as a set of three non-collinear points and the unique geodesics connecting them, and since a Riemannian manifold is equipped with an inner product, it makes sense to measure angles (and hence we may have right triangles). Let's now examine the rather complicated figure to the left. There are two semicircular geodesics (one with a radius of 1) and two vertical geodesics such that the angle at \(C\) is a right angle. We will need the following facts from the properties of hyperbolic space that we have already covered:
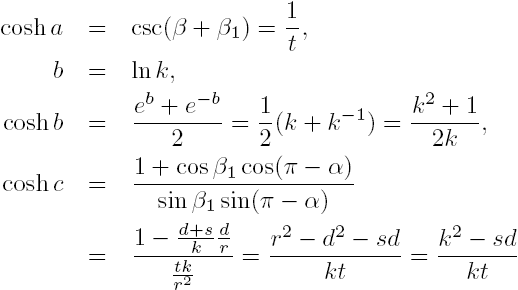
Now, we also know that \(s^2+t^2=1\) and \((s+d)^2+t^2=r^2=d^2+k^2\), so we have the Hyperbolic Pythagorean Theorem:

Note that for very small side lengths, we can approximate the last expression to get

which is the Pythagorean Theorem (as we would expect: since \(\mathbb{H}^2\) is a manifold, it must be locally Euclidean).
General Triangles
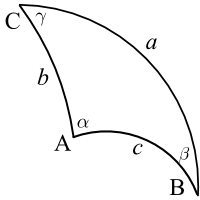
In addition to the Pythagorean Theorem, we can derive the corresponding hyperbolic formulas for other plane geometry relations you may remember from high school, such as the Law of Sines or Law of Cosines. Using the above relations:
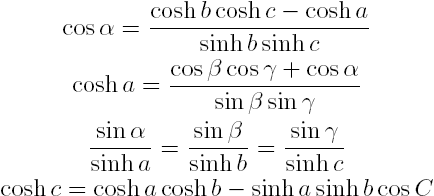
Previous Page |
Next Page |